Zadanie 8

Najneskorší termín odovzdania: 13.4.2025 (nedeľa) o 18:00
Odovzdávané súbory: OneWay.java, Minimum.java

Jednosmerky (5 bodov)

Aupark konečne stojí a na základe zmluvy s mestom ostáva investorovi zrealizovať už len rekonštrukciu niekoľkých križovatiek. Vyvrcholením tejto rekonštrucie je vybudovanie niekoľkých mestských okruhov. Väčšina z tých okruhov vznikne zjednosmernením ulíc v meste. Novému vedeniu mesta sa ale táto myšlienka jednoSMERiek natoľko zapáčila, že mesto poverilo dopravných expertov, aby na tomto princípe navrhlo ďalšie zjednosmernenia ulíc s cieľom zlepšiť dopravnú situáciu v meste. Dopravní experti neváhali a zjednosmerňovali každú ulicu, ktorá sa aspoň trochu dala zjednosmerniť. Keď už boli s výsledkom práce spokojní, predložili vedeniu mesta svoj návrh. I tu múdre vedenia mesta položilo otázku: Budú sa môcť občania mesta dostať na každé miesto v meste autom po zjednosmernení ulíc? V radoch dopravných expertov nastal šum a vrava. Nevedeli odpovedať.

Úloha: Daný je plán ulíc mesta po plánovanom zjednosmernení vybraných ulíc. Vytvorte program, ktorý overí, či sa v novom pláne mesta bude dať z každého miesta (križovatky) do každého iného miesta (križovatky) v meste.

Vstup: Súbor, v ktorom prvý riadok obsahuje dvojicu medzerou oddelených čísel N a M, kde N je počet križovatiek v meste a M je počet ulíc v meste (1 ≤ N ≤ 80). Križovatky sú očíslované od 0 po N-1. Každá ulica spája nejaké dve križovatky. Ďalej bude nasledovať M riadkov popisujúcich ulice v meste. Každý riadok obsahuje medzerami oddelené dve čísla a písmeno. Prvé číslo je číslo križovatky, na ktorej ulica začína. Druhé číslo je číslo križovatky, na ktorej ulica končí. Písmeno J označuje, že ulica je jednosmerná. Naopak písmeno O označuje, že ulica je obojsmerná.

Výstup: true alebo false, podľa toho, či je možné sa ulicami mesta dostať autom z ľubovoľnej križovatky na ľubovoľnú inú križovatku.

Príklad:

1
2
3
4
5
6
7
8
9
10
11
12
vstup:

6 8

1 2 O

2 3 O

1 3 O

1 4 J

3 4 J

4 5 J

5 0 O

0 4 J

vystup: 

false

1
2
3
4
5
6
7
8
9
10
11
12
vstup:

6 8

1 2 O

2 3 O

1 3 O

1 4 J

3 4 O

4 5 J

5 0 O

0 4 J

vystup: 

true

1
2
3
4
5
6
7
8
9
import java.io.*;



public class OneWay {



    public boolean solve(File input) {

        return false;

    }



}

Minimum (10 bodov)

Vďaka napredovaniu technológie snímania ľudského tela je dnes možné sledovať aj priebeh laparoskopickej operácie a kontrolovať jej priebeh priebežnými snímkami. Lekári univerzitnej nemocnice (na Slovensku) sú samozrejme nútení používať tieto snímky podľa možností čo najmenej, aby sa minimalizovali náklady na liečbu. U jedného pacienta potrebujú vykonať odber z nálezu-útvaru objaveného na snímke, pričom ale chcú celý priebeh dokumentovať snímkami (aby to mohli publikovať v lekárskom časopise). Ponúka sa im viacero možných vstupov, potrebovali by zistiť koľko najmenej snímok musia urobiť, ak chcú zaznamenať pohyby operatívneho nástroja v maximálnom rozlíšení snímacieho prístroja (Keďže snímacie zariadenie je rastrové, pohyb nástroja je možný v jednom z ôsmich smerov.).
Pomôžte im napísať program, ktorý nájde najmenší počet snímok potrebných na zaznamenanie pohybov lekárskeho nástroja v tele človeka na odber tkaniva z nálezu, ak lekári určili niekoľko možných vstupov.

Vstup: Prvý riadok vstupu obsahuje dve celé čísla 1 ≤ N, M ≤ 100, rozmery snímky. Nasleduje N riadkov obsahujúcich M znakov popisujúcich jeden riadok snímky s nasledovným významom:

• . prázdne políčko
• ? možný vstup
• # prekážka (kosť, vnútorný orgán)
• * nález

Môžete predpokladať, že vstup je korektný (neobsahuje iné znaky, obsahuje po aspoň jednom znaku ? aj *)

Výstup: jedno nezáporné celé číslo – najmenšia vzdialenosť. Ak pohyb zo žiadneho vstupu k nálezu nie je možný, tak vráti nulu.

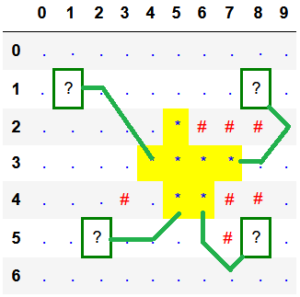
Príklad: Pre nasledujúci vstupný súbor je výsledok 3.

1
2
3
4
5
6
7
8
7 10

..........

.?......?.

.....*###.

....****..

...#.**##.

..?....#?.

..........

1
2
3
4
5
6
7
8
import java.io.*;



public class Minimum {



    public int solve(File input) {

        return 0;

    }

}

Prehľadávanie do šírky s pridanou informáciou o vzdialenosti. Štartovacích vrcholov môže byť v rade na začiatku viacero. Algoritmus je možné ukončiť pri nájdení prvého nálezu.