Kód z prednášky
Ciele cvičení:
- vedieť, ako v programoch uložiť a reprezentovať hierarchické údaje a štruktúry,
- vedieť riešiť jednoduché úlohy s hierarchickými údajovými štruktúrami,
- zoznámiť sa s aritmetickými stromami,
- poznať binárne vyhľadávacie stromy a základné operácie nad nimi (test na prítomnosť hodnoty, pridanie a odobranie hodnoty),
- vedieť analyzovať časovú zložitosť jednotlivých algoritmov.
Strom potomkov
- Do triedy
Osoba z prednášky pridajte metódu pocetGeneracii, ktorá vráti počet generácií potomkov danej osoby.
1
| public int pocetGeneracii(); |
- Do triedy
Osoba z prednášky pridajte metódu pridajDoZoznamu, ktorá uloží všetky osoby stromu potomkov danej osoby do zoznamu osôb.
1
| public void pridajDoZoznamu(List<Osoba> zoznam); |
Súbory
- Naprogramujte metódu, ktorá zráta celkovú veľkosť súborov, ktoré sa nachádzajú v zadanom adresári a jeho podadresároch.
1
| public long velkostSuborov (File adresar ); |
Binárne stromy
- Nakreslite nejaký binárny strom s 10 uzlami s číselnými hodnotami v uzloch. Popíšte tento strom z hľadiska „stromových“ parametrov (výška, koreň, listy, vnútorné uzly, …).
- Do triedy
Uzol (z prednášky) pridajte statickú metódu, ktorá vráti referenciu na koreň stromu, ktorého opis je v zadanom reťazci.
1
| public static Uzol stromZRetazca (String opisStromu ) |
Opis stromu je reťazec tvaru: (L) h (P), kde L je opis ľavého podstromu, P je opis pravého podstromu a h je hodnota v koreni stromu.
Reťazec ((2) 7 ((5) 6 (11))) 2 (5 ((4) 9)) reprezentuje strom:
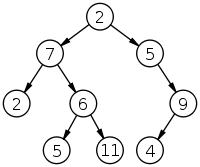
- Do triedy
Uzol (z prednášky) pridajte metódu ktorá pre zadaný uzol vráti súčet hodnôt uložených v uzloch stromu, ktorého je zadaný uzol koreňom.
- Do triedy
Uzol (z prednášky) pridajte metódy na výpočet minimálnej uloženej hodnoty, počtu uložených hodnôt a výšku stromu.
- Predpokladajte, že poznáte postupnosť inorder a preorder spracovania hodnôt v binárnom strome, ktorý v každom uzle uchováva inú hodnotu. Navrhnite postup, ako zo znalosti týchto 2 postupností zrekonštruovať binárny strom. pre náročnejších: Ako by ste túto úlohu riešili pri znalosti postupností postorder a preorder prechodu?
- Aký je minimálny a maximálny počet uzlov stromu s výškou
h? Svoje tvrdenie dokážte (formálny dôkaz matematickou indukciou na výšku stromu h).
- Dôsledok: Aká je minimálna možná výška a aká je maximálna možná výška binárneho stromu s
n uzlami?
Binárne vyhľadávacie stromy
- Pre náhodné vytvorenú postupnosť 10 čísel nakreslite binárny strom uchovávajúci tieto hodnoty, ktorý je navyše aj binárnym vyhľadávacím stromom.
- Odsimulujte algoritmy na testovanie prítomnosti hodnoty, pridávanie a odoberanie hodnoty.
- Navrhnite (a implementujte) algoritmus na overenie, či nejaký binárny strom je binárny vyhľadávací strom.
- Akú postupnosť hodnôt dostaneme pri inorder prechode binárneho vyhľadávacieho stromu a prečo?
- Napíšte metódu, ktorá v binárnom vyhľadávacom strome nájde minimálnu hodnotu.
- Vyskúšajte https://people.ksp.sk/~kuko/gnarley-trees/Intro.html
- Je nižšie uvedená implementácia zistenia výskytu hodnoty v BVS korektná? Ak áno, vyargumentujte. Ak nie, nájdite taký BVS, na ktorom metóda zlyhá.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public boolean contains(int hodnota) {
Uzol aktualny = koren;
while (aktualny != null) {
if (aktualny.hodnota == hodnota)
return true;
if (hodnota < aktualny.hodnota)
aktualny = aktualny.lavy;
if (aktualny.hodnota < hodnota)
aktualny = aktualny.pravy;
}
return false;
} |
Aritmetické stromy
- Pre zadaný aritmetický výraz nakreslite prislúchajúci strom tohto výrazu.
- Čo je výsledkom postupnosti inorder (postorder) prechodu tohto stromu? Rozdiskutujte zápis výrazov v postfixovej notácii.
- Do triedy
Vyraz pridajte metódy na výpis výrazu v postfixovej notácii a vyhodnotenie výrazu.
- Pre fajnšmekrov: Rozšírte triedu
Vyraz o podporu premenných vo výraze.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
| /**
* Trieda reprezentujuca aritmeticky vyraz
*/
public class Vyraz {
/**
* Rozhranie, ktore implementuju vsetky uzly aritmetickeho stromu
*/
private interface Clen {
@Override
public String toString ();
}
/**
* Trieda implementujuca uzol stromu aritmetickeho stromu, ktory
* reprezentuje binarnu operaciu
*/
private static class BinarnaOperacia implements Clen {
private char operator ;
private Clen lavyPodvyraz ;
private Clen pravyPodvyraz ;
public BinarnaOperacia (char operator, Clen lavy, Clen pravy ) {
this. operator = operator ;
this. lavyPodvyraz = lavy ;
this. pravyPodvyraz = pravy ;
}
@Override
public String toString () {
return "(" + lavyPodvyraz. toString() + operator
+ pravyPodvyraz. toString() + ")";
}
}
/**
* Trieda implementujuca uzol aritmetickeho stromu, ktory reprezentuje
* konstantu
*/
private static class Hodnota implements Clen {
private double hodnota ;
public Hodnota (double hodnota ) {
this. hodnota = hodnota ;
}
@Override
public String toString () {
return Double. toString(hodnota );
}
}
/**
* Symboly operacii od najnizsej priority po najvyssiu
*/
private static final String SYMBOLY_OPERACII = "+-*/";
/**
* Prevedie zadany vyraz do aritmetickeho stromu
*
* @param vyraz
* vyraz, ktory sa ma parsovat
* @return referencia na koren aritmetickeho stromu
*/
private static Clen prevedNaStrom (String vyraz ) {
// Odstranime zbytocne medzery
vyraz = vyraz. trim();
// Najdeme operator s najnizsou prioritou, ktory nie je v zatvorkach
int operatorIdx = Integer. MAX_VALUE;
int operatorPoz = -1;
int pocitadloZatvoriek = 0;
for (int i = 0; i < vyraz. length(); i ++) {
char znak = vyraz. charAt(i );
if (znak == '(')
pocitadloZatvoriek ++;
if (znak == ')')
pocitadloZatvoriek --;
int priorita = SYMBOLY_OPERACII. indexOf(znak );
if ((priorita != -1) && (pocitadloZatvoriek == 0) && (i > 0)) {
if (priorita <= operatorIdx ) {
operatorIdx = priorita ;
operatorPoz = i ;
}
}
}
// Rozdelime vyraz na podvyrazy
if (operatorPoz != -1) {
return new BinarnaOperacia (SYMBOLY_OPERACII. charAt(operatorIdx ),
prevedNaStrom (vyraz. substring(0, operatorPoz )),
prevedNaStrom (vyraz. substring(operatorPoz + 1)));
}
// Poznamka: Ak sme nenasli operator, tak je to alebo konstanta, alebo
// cely vyraz je ozatvorkovany
// Ak je cely vyraz ozatvorkovany, tak nechame rozparsovat jeho vnutornu
// cast
if ((vyraz. charAt(0) == '(')
&& (vyraz. charAt(vyraz. length() - 1) == ')'))
return prevedNaStrom (vyraz. substring(1, vyraz. length() - 1));
// Ak sme tu, tak to musi byt cislo
try {
return new Hodnota (Double. parseDouble(vyraz ));
} catch (NumberFormatException e ) {
throw new RuntimeException(
"Zadany vyraz nie je korektny aritmeticky vyraz");
}
}
/**
* Koren aritmetickeho stromu vyrazu
*/
private Clen koren ;
/**
* Skontruuje novy aritmeticky vyraz
*
* @param vyraz
* retazec s aritmetickym vyrazom
*/
public Vyraz (String vyraz ) {
koren = prevedNaStrom (vyraz );
}
@Override
public String toString () {
return koren. toString();
}
public static void main (String[] args ) {
Vyraz v = new Vyraz ("(-3)+6/2+3*2");
System. out. println(v );
}
} |
Pre fajnšmekrov:
- Formálne (=matematicky, napr. priamy dôkaz) dokážte:
- Ak limn→∞ f(n)/g(n) = c, kde
c je z R, potom f(n) = O(g(n))
- Ukážte, že predošlá implikácia nemôže byť zosilnená na ekvivalenciu tak, že skonštruujete algoritmus, ktorého časová zložitosť v najhoršom prípade na vstupe veľkosti
n je taká funkcia T(n), že T(n) = O(g(n)), ale neexistuje c z R také, že limn→∞ T(n)/g(n) = c
- Preskúmajte princípy a základné myšlienky samovyvažovacích binárnych vyhľadávacích stromov.

