Zadanie 2
Najneskorší termín odovzdania: 3.3.2024 (nedeľa) o 18:00
Odovzdávané súbory: AdamSort.java, YouTubeSort.java, SpravneZavazia.java
Doplňujúce požiadavky:
- riešenia, ktoré nebude možné skompilovať (t.j. riešenia so syntaktickými chybami) nebudú hodnotené,
- zdrojový kód správne naformátujte (CTRL+SHIFT+F),
- komentovaný zdrojový kód
Oóóóóó (2 body)
Riešenie tejto časti môžete nahrať vo vhodnom formáte do moodlu. Ideálne vyriešiť na papier, oskenovať/fotiť a odovzdať. Alebo doniesť na prednášku v pondelok 4.3.2024. Obe možnosti majú posunutý termín odovzdania na čas začiatku prednášky.
1 bod: Na cvičeniach vám cvičiaci spomínali, že pri asymptotickej časovej zložitosti na základe logaritmu nezáleží. Aby ste sa o tom presvedčili, formálne dokážte:
- 3*d*logm+2(n) = O(log2 n), kde
dje deň vášho narodenia amje mesiac vášho narodenia.
0.5 bod: Zoraďte jednotlivé funkcia podľa O-notácie tak, aby ak je funkcia f pred funkciou g, potom f = O(g). Hodnotu d nahraďte dňom vášho narodenia a hodnotu m mesiacom vášho narodenia.
- n + d6
- 2*n4 – m*n
- 2n-2
- (d+3)*n + log(n)
- n3*log10(n)
- nm+6
+0.5 boda: Aspoň pre jednu dvojicu týchto funkcií formálne dokážte, že f = O(g).
Poznámka: Pri formálnom zdôvodnení sa očakávajú pekné dôkazy. Hodnotitelia majú základy logiky (zvládajú logické operátory a logické výrazy), pokiaľ ide o všeobecnú matematiku, tu zvládajú len na úrovni základnej školy. Takže dajte si pozor na to, čo prehlásite ako zrejmé.
YouTubeSort (1 bod)
Vedeli ste, že folklór a algoritmy nemajú od seba až tak ďaleko? Nuž pozrite si video s tanečnou vizualizáciou triedenia výberom: http://www.youtube.com/watch?v=Ns4TPTC8whw
Ako si však niektorí všimli, tanečníci implementovali trochu iný algoritmus triedenia výberom, než bol prezentovaný na prednáške. Ako by vyzeral tento algoritmus zapísaný v Jave?
Uvažujme triedu TriediaciAlgoritmus z cvičenia.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public abstract class TriediaciAlgoritmus {
/**
* Aktualne usporiadavane pole
*/
private int[] p;
/**
* Porovna prvky v poli na zadanych indexoch
*
* @return vrati zaporne cislo, ak p[idx1] < p[idx2],
* 0, ak p[idx1]==p[idx2], a
* kladne cislo, ak p[idx1] > p[idx2]
*/
protected int porovnaj(int idx1, int idx2) {
return Integer.compare(p[idx1], p[idx2]);
}
/**
* Vymeni prvky v usporiadavanom poli na zadanych indexoch
*/
protected void vymen(int idx1, int idx2) {
int pom = p[idx1];
p[idx1] = p[idx2];
p[idx2] = pom;
}
/**
* Vypise pole
*/
protected void vypisPole() {
System.out.println(Arrays.toString(p));
}
/**
* Usporiada prvky v poli od najmensieho po najvacsie
*
* @param p
* pole, ktoreho prvky maju byt usporiadane
*/
public void utried(int[] p) {
this.p = p;
utried(p.length);
this.p = null;
}
/**
* Metoda, ktora implementuje triedenie podla urciteho algoritmu
* @param dlzkaPola dlzka (pocet prvkov) usporiadavaneho pola
*/
protected abstract void utried(int dlzkaPola);
}
Prekrytím abstraktnej metódy utried vytvorte triedu YouTubeSort, ktorá bude implementovať algoritmus triedenia výberom podľa uvedeného videa na YouTube.
2
3
4
5
6
7
8
@Override
protected void utried(int dlzkaPola) {
}
}
Geniálny algoritmus (3 body)
Adam sa zúčastnil 2. prednášky z PAZ1b, kde bolo prezentované binárne vyhľadávanie v usporiadanej postupnosti v čase O(log n), triedenie výberom a bublikové triedenie bežiace v čase O(n2).
Adam bol fascinovaný triediacimi (usporadúvacími) algoritmami. Začal googliť a na YouTube našiel aj tieto videá:
Keď ich tak pozeral, chytrý algoritmus analyzujúci „divákov“ na YouTube sa rozhodol Adamovi odporučiť na pozretie aj toto video: http://www.youtube.com/watch?v=k4RRi_ntQc8 Jeho pozretie výrazne zmenilo Adamov život (teda aspoň na pár najbližších hodín). Keď Obama tvrdí, že BubbleSort (bublinkové triedenie) nie je ta správna cesta ako „sortovať“, znamená to, že musí existovať niečo lepšie (čo určite FBI, CIA, NSA a ktovie kto ešte pred svetom dôkladne strážia). Pred Adamom teraz stála jasná výzva: nájsť lepší algoritmus. Po intenzívnom rozmýšľaní prišiel s geniálnou stratégiou pre triediaci algoritmus, ktorý by mal mať asymptoticky lepšiu časovú zložitosť ako triedenie výberom, či bublinkové triedenie. Jeho stratégia vychádzala z tejto úvahy:
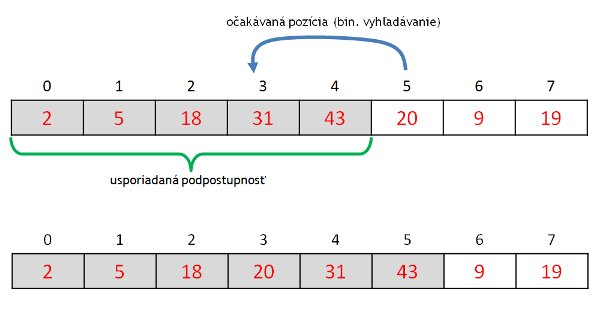
Predpokladajme, že máme utriediť n čísel. Riešme teda menší problém a nejako rekurzívne utrieďme n-1 čísel. Konkrétne, rekurzívne utrieďme prvých n-1 čísel v poli a číslo na poslednom indexe nechajme tak. Aby sme dostali utriedenú postupnosť n čísel, ostáva nám už len umiestniť číslo na poslednom indexe na správne miesto. Nuž a toto miesto (index) vieme predsa nájsť binárnym vyhľadávaním v čase O(log n). Celková zložitosť algoritmu by tak mala byť lepšia, pretože to, čo vlastne robíme je, že n krát vkladáme číslo (najprv na indexe 0, potom 1, 2, …, n-1) do nejakej už utriedenej postupnosti s využitím binárneho vyhľadávania s logaritmickou časovou zložitosťou.
2 body: Na základe Adamovej myšlienky implementujte nerekurzívny triediaci algoritmus (metóda utried v nižšie uvedenej triede AdamSort).
1 bod: Analyzujte Adamov algoritmus. Bude jeho stratégia fungovať, t.j. budú sa dať nejako takto utriediť čísla? Akú časovú zložitosť bude mať algoritmus založený na tejto stratégii? Je pravda, že sa mu podarí skonštruovať algoritmus, ktorý bude asymptoticky lepší ako triedenie výberom alebo bublinkové triedenie? Svoje odpovede zdôvodnite a podporte argumentami. V písomnej podobe ich odovzdajte cez Moodle (ako komentár k odoslanej implementácii triedy AdamSort alebo ako samostatný textový súbor).
Poznámka: Ako odpovedať stručne na otázky o časovej zložitosti (samozrejme v prípade, že algoritmus funguje)?
- Časová zložitosť Adamovho algoritmu v najhoršom prípade je
O(T(n)), pretože … - Záver:
- Ak T(n) = n2, potom Adamov algoritmus má rovnakú asymptotickú zložitosť ako triedenia z prednášky.
- Ak T(n) nie je v O(n2), potom Adamov algoritmus má asymptoticky horšiu časovú zložitosť ako algoritmy z prednášky.
- Ak n2 nie je v O(T(n)), potom Adamov algoritmus má asymptoticky lepšiu časovú zložitosť než algoritmy z prednášky.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
public class AdamSort {
/**
* Vrati index v poli p, kde by sa mal nachadzat prvok so zadanou hodnotou v
* zadanom usporiadanom podpoli pola p.
*
* @param p
* pole
* @param odIdx
* index prveho prvku usporiadaneho podpola
* @param poIdx
* index posledneho prvku usporiadaneho podpola
* @param hodnota
* hodnota, ktoru mame v plane vlozit
* @return index pola, kde by sa mala nachadzat zadana hodnota
*/
public static int binarneHladajIndex(int[] p, int odIdx, int poIdx, int hodnota) {
// Skontrolujeme korektnost indexov
if (odIdx > poIdx)
throw new RuntimeException("Parameter odIdx musi byt mensi alebo rovny ako poIdx.");
// Ak je hodnota vacsia, ako cislo na poslednom indexe uvazovaneho
// podpola, tak vratime nasledujuci index (spravne miesto pre hodnotu je
// az za poslednym prvkom podpola)
if (p[poIdx] < hodnota)
return poIdx + 1;
// Vieme, ze spravny index je medzi odIdx..poIdx - aplikujeme binarne
// vyhladavanie
while (odIdx < poIdx) {
// Vypocitame stredovy index
int stred = (odIdx + poIdx) / 2;
if (hodnota <= p[stred]) {
// Ak je hodnota mensia alebo rovna ako hodnota v strede, tak
// spravne miesto je niekde medzi odIdx..stred
poIdx = stred;
} else {
// Ak je hodnota vacsia ako hodnota v strede, tak spravne miesto
// bude az za stredovym indexom, t.j. niekde medzi stred+1 a
// poIdx
odIdx = stred + 1;
}
}
return odIdx;
}
/**
* Specialna verzia pre Adamov algoritmus, kedze on predpoklada, ze v poli
* ma prvky na indexoch 0..poIdx uz usporiadane.
*/
public static int binarneHladajIndex(int[] p, int poIdx, int hodnota) {
return binarneHladajIndex(p, 0, poIdx, hodnota);
}
/**
* Usporiada cisla v poli od najmensieho po najvacsie
*
* @param p
* pole, ktoreho prvky treba usporiadat
*/
public static void utried(int[] p) {
// Triediaci algoritmus na zaklade Adamovej myslienky
}
/**
* @param args
*/
public static void main(String[] args) {
int[] p = new int[30];
for (int i = 0; i < p.length; i++)
p[i] = (int) (Math.random() * 1000);
System.out.println(Arrays.toString(p));
utried(p); // AdamSort.utried(p);
System.out.println(Arrays.toString(p));
}
}
Top 5 – správne závažia (0-5 bodov: pre fajnšmekrov)
Máme n závaží usporiadaných od najľahšieho po najťažšie (ich hmotnosti sú v poli zavazia). Viacero závaží môže mať rovnakú hmotnosť. Kvôli jednoduchosti predpokladáme, že hmotnosť každého závažia je celé číslo v gramoch. Implementujte metódu, ktorá vráti, či vieme vybrať nejaké 2 závažia tak, že súčet ich hmotností je presne h.
2
3
4
5
6
7
public static boolean obsahujeVyberSHmotnostou(int[] zavazia, int h) {
return true;
}
}
Úlohu ide riešiť v čase O(n2) jednoducho 2 vnorenými cyklami. Chceme ale samozrejme asymptoticky lepšie riešenia.
Počet bodov záleží od asymptotickej časovej zložitosti riešenia a argumentácie (komentároch) o funkčnosti kódu a jeho zložitosti. V prípade rovnakej asymptotickej časovej zložitosti rozhoduje aj čas nameraný pri evaluácii a kvalita argumentov dokazujúcich, že algoritmus je korektný.